Ландшафтная аэродинамическая труба ветровая нагрузка

Таблица 3. Коэффициент k для типов местности:

Расчет ветровой нагрузки по формуле

Переток воздушных масс вдоль поверхности земли происходит с разной скоростью. Натыкаясь на какое-либо препятствие, кинетическая энергия ветра преобразуется в давление, создавая ветровую нагрузку. Это усилие может ощутить любой человек, двигающийся навстречу потоку. Создаваемая нагрузка зависит от нескольких факторов:

• скорость ветрового потока;
• плотность воздушной струи,— при повышенной влажности, удельный вес воздуха становится больше, соответственно, возрастает величина переносимой энергии;
• форма стационарного объекта.

• Расчёт усилий ↓
• Расчёт ветровой нагрузки на крышу ↓
• Пример расчёта ↓
• Альтернативная энергетика ↓

В последнем случае на отдельные части строительного сооружения действуют силы, направленные в разные стороны, например:

1. На вертикальную стену действует так называемое лобовое усилие, стремящееся сдвинуть объект с места. Противостоять этому усилию помогают несколько конструктивных решений:
2. На крышу, кроме горизонтальных усилий (вдавливающих), действуют и вертикальные силы, образующиеся от разделения воздушного потока при ударе о стену. Вектор воздушного потока стремится поднять крышу, оторвать её от стен.
3. Совокупность всех этих вихревых потоков создают ветровую нагрузку не только на крупные элементы здания, но распространяет свои влияния на все элементы строительного сооружения, — двери, окна, кровлю, водостоки, антенну, дымоход.

Таблица 2.

Источник: СНиП 2.01.07-85 (с изм. 1 1993)Давление ветровой нагрузки определяется по формуле:где Wo- нормативное значение давления (см. таб.1)
k — коэффициент, учитывающий изменение ветрового давления по высоте, определяется по таб.2 в зависимости от типа местности. Принимаются следующие типы местности:

• А — открытые побережья морей, озёр и водохранилищ, пустыни, лесостепи, тундра;
• В — городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой не более 10 м;
• С — городские районы с застройкой зданниями высотой более 25 м.

с — аэродинамический коэффициент.где V₀ -численно равно скорости ветра, м/с, на уровне 10 м над поверхностью земли для местности типа А, соответствующей 10-минутному интервалу осреднения и превышаемой в среднем раз в 5 лет (если техническими условиями, утверждёнными в установленном порядке, не регламентированы другие периоды повторяемости скоростей ветра).Таблица 1.Таблица 2.

Высота z,м	коэффициент k для типов местности
	A	B	C
480	2,75	2,75	2,75

Таблица 3.

Высота z,м	Коэффициент пульсаций давления ветра z для типов местности
	A	B	C
£ 5	0,85	1,22	1,78
10	0,76	1,06	1,78
20	0,69	0,92	1,5
40	0,62	0,8	1,26
60	0,58	0,74	1,14
80	0,56	0,7	1,06
100	0,54	0,67	1
150	0,51	0,62	0,9
200	0,49	0,58	0,84
250	0,47	0,56	0,8
300	0,46	0,54	0,76
350	0,46	0,52	0,73
³ 480	0,46	0,5	0,68

Таблица 4. Определение аэродинамического коэффициента для разных типов сооружений

b , град	0	15	3	45	60	75	90
с	1	0,8	0,4	-0,2	-0,8	-1,2	-1,25
b , град	105	120	135	150	175	180
с	-1	-0,6	-0,2	0,2	0,3	0,4

4.2. Призматические сооружения

l	5	10	20	35	50	100	беск.
k	0,6	0,65	0,75	0,85	0,9	0,95	2

В табл. 2 приведены значения скорости ветра в условиях городского центра, рассчитанные по формуле (3). Значения скорости ветра на высоте 10 м приняты равными расчетным значениям, приведенным для г. Москвы в СНиП 2.04.05 «Отопление, вентиляция и кондиционирование» (для холодного периода года: параметр А – v₀ = 4,7 м/с, параметр Б – v₀ = 4 м/с; для теплого периода года: параметры А и Б – v₀ = 1 м/с).

Аэродинамика высотных зданий

Ю. А. Табунщиков, профессор, доктор техн. наук, член-корр. РААСН;В предлагаемой ниже статье изложены предложения по расчетным наружным климатическим параметрам для проектирования систем ОВК и теплозащиты высотных зданий, а также результаты исследования аэродинамики высотных зданий. Значения расчетных климатических параметров являются оригинальными и рассматриваются на примере климатических условий г. Москвы. Аэродинамические исследования обобщают результаты ряда международных проектов.

Введение

Вопросы аэродинамики зданий всегда считались достаточно важными, а в ряде случаев – определяющими для проектирования вентиляции зданий и расчета воздушных потоков внутри здания, оценки влияния здания на аэродинамический режим прилегающей территории, выбора ограждающих конструкций с необходимой воздухопроницаемостью. Кроме того, внутри зданий могут возникать сильные воздушные потоки, что требует специальных решений: шлюзования входных дверей, лестничных секций, герметизации мусоропроводов и т. д. Есть еще ряд вопросов, который связан с аэродинамикой зданий, в том числе рассеивание вредностей, расположение пешеходных дорожек, образование снегозаносов и т. п.Аэродинамика высотных зданий имеет свою специфику, т. к. для них влияние наружных климатических воздействий и величины градиентов перемещения потоков массы и энергии внутри здания являются по своей значимости экстремальными.

Изменение по высоте температуры,скорости ветра и барометрического давления

Известно, что в холодный и теплый период года температура наружного воздуха понижается примерно на 1 °С через каждые 150 м высоты, атмосферное давление понижается примерно на 1 гПа через каждые 8 м высоты, а скорость ветра увеличивается [2].Изменение по высоте температуры и атмосферного давления описываются следующими формулами [2]:p_h = p₀ (1 – 2,25577×10 –5 x h) 5,2559 , (2)где t_h, p_h – соответственно температура, °С, и давление, Па, на высоте h, м;t₀, p₀ – соответственно температура, °С, и давление, Па, у поверхности земли;В табл. 1 приведены значения температуры наружного воздуха и наружного барометрического давления, рассчитанные по формулам (1) и (2). В табл. 1 значения температуры и барометрического давления у поверхности земли приняты равными расчетным значениям, приведенным для г. Москвы в СНиП 2.04.05 «Отопление, вентиляция и кондиционирование» (для холодного периода: параметр А – расчетное значение температуры наружного воздуха t₀ = –15 °С, а параметр Б – расчетное значение температуры наружного воздуха t₀ = –26 °С; для теплого периода: параметр А – расчетное значение температуры наружного воздуха t₀ = 22,3 °С, параметр Б – расчетное значение температуры наружного воздуха t₀ = 28,5 °С; барометрическое давление p₀ = 990 гПа).Для оценки изменения скорости ветра по высоте используются различные модели – спираль Экмана, логарифмический закон, степенной закон [1, 2, 7, 9]. Эти модели позволяют оценить скорость ветра v на высоте h, если известна скорость ветра v₀ на высоте h₀. Например, степенной закон изменения скорости ветра по высоте имеет вид [2, 7, 9]:где v_h – скорость ветра, м/с, на высоте h, м;v₀ – скорость ветра, м/с, измеренная на высоте h₀, м (как правило, скорости ветра измеряются на высоте 10–15 м, и в этом случае h₀ = 10—15 м);a – показатель степени, зависящий от типа местности и устанавливаемый экспериментально; в [2] рекомендуется для центров крупных городов принимать a = 0,33.В табл. 2 приведены значения скорости ветра в условиях городского центра, рассчитанные по формуле (3). Значения скорости ветра на высоте 10 м приняты равными расчетным значениям, приведенным для г. Москвы в СНиП 2.04.05 «Отопление, вентиляция и кондиционирование» (для холодного периода года: параметр А – v₀ = 4,7 м/с, параметр Б – v₀ = 4 м/с; для теплого периода года: параметры А и Б – v₀ = 1 м/с).Вместе с тем часто известна скорость ветра, измеренная на метеорологической станции, которая располагается, как правило, на открытой местности. В условиях плотной городской застройки скорость ветра на той же высоте будет ниже. Скорость ветра v на высоте h в зависимости от типа местности в модели степенного закона рассчитывается по формуле [2, 9]: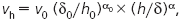

(4)где v_h – скорость ветра, м/с, на высоте h, м, на местности, тип которой характеризуется показателем степени a и толщиной пограничного слоя d ;v₀ – скорость ветра, м/с, измеренная на высоте h₀, м, на местности, тип которой характеризуется показателем степени a₀ и толщиной пограничного слоя d ₀;a – показатель степени, зависящий от типа местности и устанавливаемый экспериментально;d – толщина пограничного слоя, м, для рассматриваемого типа местности; в работе [2] рекомендуется следующие значения a и d :Ј для центров крупных городов a = 0,33, d = 460 м;Ј для условий пригорода (в данном случае под пригородом понимается местность, в которой в радиусе 2 000 м расположена малоэтажная застройка или лесопарковые массивы) a = 0,22, d = 370 м;Ј для открытой местности a = 0,14, d = 270 м.a ₀, d ₀ – показатель степени и толщина пограничного слоя для местности, на которой зафиксирована скорость ветра v₀; как правило, скорости ветра измеряются на метеорологических станциях, расположенных на открытой местности на высоте 10–15 м, и в этом случае h₀ = 10—15 м, a ₀ = 0,14, d ₀ = 270 м.Под пограничным слоем понимается приземной слой атмосферы, в котором поверхность земли оказывает тормозящее воздействие на движущую массу воздуха. Возрастание скорости ветра происходит в пределах пограничного слоя, выше пограничного слоя (в свободной атмосфере) скорость ветра постоянна (градиентная скорость). Толщина пограничного слоя в общем случае зависит от состояния атмосферы, типа местности, широты местности и силы ветра; в рассмотренной выше методике принимается инженерное допущение – толщина пограничного слоя зависит только от типа местности, т. е. d является функцией только аргумента a .По формуле (4) были выполнены расчеты ожидаемых скоростей ветра для трех типов местности – открытого пространства, пригорода и центра крупного города с плотной застройкой. Значения скоростей ветра для открытой местности, зафиксированных на высоте 10 м (h₀ = 10 м a ₀ = 0,14, d ₀ = 270 м), были приняты равными v₀ = 1 м/с, 5 м/с и 10 м/с. Результаты расчетов представлены в табл. 3 и на рис. 1.Высокие значения скорости ветра на больших высотах, как правило, изменяют угол падения дождевых капель, так что увеличивается количество дождя, падающего на вертикальные поверхности здания. Это может явиться причиной переувлажнения вертикальных ограждающих конструкций. Исследования зависимости угла падения атмосферных осадков различной интенсивности от скорости ветра были проведены А. И. Кругловой и изложены в [6].Изменение скорости ветра по высоте в зависимости от типа местности

Конвективные воздушные потоки у наружной поверхности здания

В теплый период года в солнечные дни из-за облученности наружных поверхностей здания солнечной радиацией их температура резко возрастает и значительно отличается от температуры окружающего воздуха. В результате разности температур образуется конвективный тепловой поток, направленный вверх здания, и имеет место так называемый приповерхностный (пограничный) слой нагретого воздуха. Разность температур наружной поверхности здания и окружающего воздуха зависит от величины солнечной радиации и коэффициента поглощения солнечной радиации материалом наружной поверхности ограждающих конструкций здания.Проведенные нами расчеты показали, что в условиях г. Москвы при безоблачном небе в июле ожидаемые максимальные температуры наружной поверхности ограждающих конструкций различной ориентации достигают значений, приведенных в табл. 4.Большое значение для проектирования воздухозаборных устройств и определения воздухопроницаемости ограждающих конструкций имеют значения скорости воздушных потоков у наружной поверхности зданий, обусловленные указанной выше разностью температур (рис. 2). На графиках (рис. 3) приведены зависимости скоростей воздуха у наружных поверхностей здания, полученные зарубежными исследователями [7].Пример эпюры скоростей восходящих воздушных потоков у наружной поверхности высотного здания, возникающих под действием разности температур D t = 20 °СМаксимальные значения скорости восходящих воздушных потоков у наружной поверхности здания

Ветровое давление, аэродинамические коэффициенты

При изучении аэродинамики зданий в [2] под высотным понимается такое здание, высота которого превышает ширину подветренного фасада в три и более раз. На рис. 4 приведены данные о распределении аэродинамических коэффициентов на фасаде квадратного в плане высотного здания при различных направлениях ветра [2].Значения аэродинамических коэффициентов на фасаде квадратного в плане высотного здания при различных направлениях ветраРассмотрение значений аэродинамических коэффициентов на фасаде квадратного в плане высотного здания при различных направлениях ветра показывает, что, если направление ветра перпендикулярно фасаду здания (рис. 4а), аэродинамические коэффициенты на этом фасаде положительны и их значения уменьшаются по направлению к боковым фасадам здания и по направлению к верхней части рассматриваемого фасада. На увеличение значения аэродинамических коэффициентов у верхней части фасада высотного здания также влияет повышение скорости ветра с увеличением высоты. Если направление ветра отклоняется от нормали к фасаду, область максимального давления смещается к наветренному углу здания (рис. 4б—в). При отклонении направления ветра от нормали на угол 45° давления становятся отрицательными у дальнего (по отношению к направлению ветра) угла фасада (рис. 4г). Если угол отклонения направления ветра от нормали лежит в пределах 60–75°, давления отрицательны по всему фасаду (рис. 4д—е). Максимальные отрицательные давления наблюдаются в областях, расположенных на боковых (по отношению к направлению ветра) фасадах у наветренных углов (рис. 4ж), причем на боковых фасадах распределение давлений существенно меняется в зависимости от относительных размеров данных фасадов (отношения высоты и ширины). Для заветренных фасадов (направление ветра составляет с нормалью угол больше 100°) значения давлений в различных областях меняются не столь существенно (рис. 4з-н).Графики изменения средних значений аэродинамических коэффициентов на фасаде прямоугольного в плане высотного здания при различных соотношениях боковых сторон в зависимости от направления ветраГрафики изменения средних значений аэродинамических коэффициентов на покрытии прямоугольного в плане высотного здания при различных соотношениях боковых сторон в зависимости от направления ветраТаким образом, если фасад расположен под углом от 0 до 60° относительно направления ветра, то среднее давление на фасаде положительно; если этот угол составляет 60–180°, то среднее давление – отрицательно. На рис. 5 приведены графики изменения средних значений аэродинамических коэффициентов на фасаде прямоугольного в плане высотного здания при различных соотношениях боковых сторон в зависимости от направления ветра [2].Графики изменения средних значений аэродинамических коэффициентов на покрытии прямоугольного в плане высотного здания (в случае, если покрытие плоское или его уклон достаточно мал) при различных соотношениях боковых сторон в зависимости от направления ветра приведены на рис. 6. Следует отметить, что, если направление ветра составляет с фасадом здания угол порядка 45°, у наветренных кромок покрытия возникают сильные завихрения (рис. 7). Высокие скорости воздушного потока в этих завихрениях обуславливают достаточно сильное разрежение (отрицательное давление) у краев покрытия, что, например, в случае сильных ветров может быть опасно для инженерного оборудования, расположенного в этой зоне.Схемы воздушных потоков, возникающие вследствие ветрового напора, направленного под углом 45° к фасаду зданияЕсли форма здания отличается от прямоугольной, характер распределения аэродинамических коэффициентов на его фасадах может существенно отличаться от приведенных выше. Возможны два метода исследования аэродинамики здания: метод физического моделирования и метод математического моделирования. Физическое моделирование здания осуществляется в аэродинамической трубе. Обычно это моделирование выполняется с учетом существующей застройки. Теория физического моделирования разработана в значительной степени благодаря работам отечественных ученых – Л. И. Седова, Т. А. Афанасьевой-Эренфест, М. В. Кирпичева, А. А. Гухмана, Э. И. Реттера, Ф. Л. Серебровского и ряда других специалистов. Более широкий список источников содержится, например, в книге Э. И. Реттера [3]. Математическое моделирование — менее надежный способ исследования аэродинамики здания с учетом застройки в связи с тем, что одновременно существуют ламинарные, турбулентные, вихревые и т. п. зоны движения, для каждой из которых необходимо иметь значения коэффициентов, характеризующих движение в этих зонах, связь между ними и характер застройки. С появлением мощной, легко доступной компьютерной техники для специалистов по математическому моделированию аэродинамики появилась возможность существенно повысить надежность расчетов.8) Распределение аэродинамических коэффициентов по периметру здания при юго-западном направлении ветра9) Распределение аэродинамических коэффициентов по периметру круглой в плане башни здания при юго-западном направлении ветра (данные математического моделирования и исследований модели здания в аэродинамической трубе)10) Распределение аэродинамических коэффициентов по периметру здания при северо-восточном направлении ветра11) Распределение аэродинамических коэффициентов по периметру квадратной в плане башни здания при северо-восточном направлении ветра (данные математического моделирования и исследований модели здания в аэродинамической трубе)В качестве примера приведены результаты математического моделирования аэродинамики высотного здания «MAIN TOWER», расположенного во Франкфурте-на-Майне, Германия [10]. Это здание достаточно сложной формы в плане представляет собой две башни – квадратную и круглую; его высота составляет 200 м.Преобладающими для Франкфурта-на-Майне являются ветры юго-западного и северо-восточного направлений. На рис. 8 и 9 показано распределение аэродинамических коэффициентов по периметру здания при воздействии юго-западного ветра. При воздействии на здание ветра северо-восточного направления характер распределения аэродинамических коэффициентов по периметру здания существенно меняется (рис. 10 и 11). В этом случае только на одном из фасадов (восточной ориентации) квадратной в плане башни здания «MAIN TOWER» аэродинамические коэффициенты положительны; на остальных фасадах они отрицательны.Значения аэродинамических коэффициентов, полученные методами математического моделирования, в дальнейшем были проверены при исследовании модели здания в аэродинамической трубе (экспериментальные значения отмечены на рис. 9 и 11 точками). Сравнение результатов, полученных методом математического моделирования и методом физического моделирования, показало их достаточно хорошую сопоставимость.Высотные здания Франкфурта-на-Майне в районе улицы Neuen Mainzer Strabe. Слева направо: «Bu..rohaus an der alten Oper» (89 м), «Eurotheum» (110 м), «MAIN TOWER» (200 м), «Garden Towers» (127 м), «Commerzbank» (259 м), «Taunustor Japan-Center» (115 м)Как было отмечено выше, режим обтекания здания воздушным потоком, помимо формы самого здания, существенно зависит от расположенных рядом других зданий и сооружений, особенностей рельефа местности и т. д. Это влияние особенно заметно, если окружающие объекты расположены на расстоянии, менее чем в пять раз превышающем высоту здания. В частности в городских условиях, сложившихся во Франкфурте-на-Майне, высотные здания, расположенные рядом в большом числе, оказывают друг на друга значительное влияние. Это взаимное влияние очень сложно рассчитать, и основным инструментом исследования становятся испытания в аэродинамической трубе.В результате при исследовании аэродинамики здания «MAIN TOWER» учитывалось взаимное влияние зданий, расположенных вдоль улицы Neuen Mainzer Strabe. Это высотные здания «Bu..rohaus an der alten Oper» (89 м), «Eurotheum» (110 м), «Garden Towers» (127 м), «Commerzbank» (259 м), «Taunustor Japan-Center» (115 м), а также прилегающая малоэтажная застройка (рис. 12).Расположение моделей зданий на поворотном столе1 — «Commerzbank» (259 м); 2 — Старое здание «Commerzbank» (110 м); 3 — «Taunustor Japan-Center» (115 м); 4 — «Garden Towers» (127 м); 5 — «MAIN TOWER» (200 м); 6 — Малоэтажная застройка (до 37 м);
7 — «Eurotheum» (110 м); 8 — «Bu..rohaus an der alten Oper» (89 м)Схема типичного распределения воздушных потоков у здания «MAIN TOWER» и в прилегающей городской застройке при юго-западном ветре
(1 — здание «Eurotheum», 110 м; 2 — здание «MAIN TOWER», 200 м; 3 — здание «Garden Towers», 127 м)Для исследований в аэродинамической трубе использовались модели в масштабе от 1:300 до 1:100. Масштаб определялся размерами исследуемой городской зоны (среды застройки) и возможностями аэродинамической трубы. В ходе испытаний модели располагались на поворотном столе, что позволило изучить характер распределения воздушных потоков при изменении направления ветра (рис. 13).Для качественной оценки распределения воздушных потоков вблизи поверхности зданий и на уровне улиц, прилегающих к зданию, применялась визуализация воздушных потоков посредством дыма. На основе полученных в ходе экспериментов в аэродинамической трубе результатов были построены схемы воздушных потоков у здания «MAIN TOWER» и в прилегающей городской застройке при различных направлениях ветра. Схема воздушных потоков при юго-западном ветре представлена на рисунке 14. Можно отметить, что при этих условиях между зданиями наблюдается ускорение воздушного потока, что приводит к понижению давления в этой зоне.Распределение аэродинамических коэффициентов на отметке 93 м с учетом влияния соседних зданий при юго-западном ветреДля количественной оценки аэродинамических коэффициентов на модели здания были размещены датчики давления. На рис. 15 показано распределение аэродинамических коэффициентов на отметке 93 м с учетом влияния соседних зданий при юго-западном ветре. Сравнение рис. 8 и 15 показывает, что из-за влияния соседних зданий характер распределения аэродинамических коэффициентов отличается от случая, когда рассматривалась модель только здания «MAIN TOWER».Относительные скорости воздушных потоков, зафиксированных датчиками, размещенными у модели здания (датчики 1—6 расположены на высоте 1,8 м)Для изучения воздушных потоков в зонах, прилегающих к зданию, датчики были размещены на модели на уровне улицы (отметка 1,8 м) и у покрытий окружающих зданий. На рис. 16 представлены скорости воздушных потоков, зафиксированных датчиками, по отношению к средней скорости господствующего ветра 3,3 м/с. Скорости воздушных потоков фиксировались при различных направлениях ветра. Исследования показали, что на уровне улицы скорости воздушных потоков уменьшаются: их численные значения составляют приблизительно 2,0–2,6 м/с. Между соседними зданиями скорости воздушных потоков возрастают, однако при низких скоростях набегающего потока (слабых ветрах) возрастание скорости воздушных потоков между соседними зданиями относительно невелико. Если средняя скорость господствующего ветра составляет 3,3 м/с, скорость воздушного потока между зданиями возрастает примерно до 4,0–4,6 м/с.

Литература

1. Серебровский Ф. Л. Аэрация жилой застройки. М., 1971.2. ASHRAE Handbook. Fundamentals. SI Edition. 1997.3. Реттер Э. И., Стриженов С. И. Аэродинамика зданий. М., 1968.4. Реттер Э. И. Архитектурно-строительная аэродинамика. М., 1984.5. Реттер Э. И. Аэродинамическая характеристика промышленных зданий. Челябинск, 1959.6. Круглова А. И. Климат и ограждающие конструкции. М., 1964.7. Daniels K. The Technology of Ecological Building. Birkhauser, 1997.8. Тарабанов М. Г. Опыт проектирования систем вентиляции и кондиционирования воздуха высотных зданий // АВОК. 2004. № 6.9. Симиу Э., Сканлан Р. Воздействие ветра на здания и сооружения. М., 1984.10. Табунщиков Ю. А., Бродач М. М., Шилкин Н. В. Энергоэффективные здания. М.: АВОК-ПРЕСС, 2003.11. Battle McCarthy Consulting Engineers. 1999. Wind Towers – Detail in Building Academy Editions. New York: John Wiley & Sons Ltd.Поделиться статьей в социальных сетях:

Аэродинамические трубы — это большие трубы, через которые проходит воздух. Туннели используются для имитации действий объекта, летящего по воздуху или движущегося по земле. Исследователи используют аэродинамические трубы, чтобы узнать больше о том, как будет летать самолет. НАСА использует аэродинамические трубы для тестирования масштабных моделей самолетов и космических кораблей. Некоторые аэродинамические трубы достаточно велики, чтобы вместить полноразмерные версии автомобилей. Аэродинамическая труба перемещает воздух вокруг объекта, создавая впечатление, будто объект действительно летит.

История

Происхождение

Английский военный инженер и математик Бенджамин Робинс (1707–1751) изобрел аппарат с вращающейся рукой для определения лобового сопротивления и провел некоторые из первых экспериментов в теории авиации. Сэр Джордж Кэли (1773–1857) также использовал вращающуюся руку для измерения сопротивления и подъемной силы различных профилей. Его вращающаяся рука была 5 футов (1,5 м) в длину и развивала максимальную скорость от 10 до 20 футов в секунду (от 3 до 6 м / с). Отто Лилиенталь использовал вращающуюся руку для точного измерения профиля крыла с различными углами атаки , создавая полярные диаграммы их отношения подъемной силы к сопротивлению , но не имел понятия наведенного сопротивления и чисел Рейнольдса .

Ниже будут показаны варианты расчета башни на действие пульсационной составляющей ветровой нагрузки с учетом суммирования по формам колебаний и без него. Сравниваться будет НДС схемы при определении величины ветровой пульсации «ручным» способом (см. выше) и программно.

Моделирование воздействия ветра в ЛИРА-САПР

При конечноэлементном моделировании башня представляется пространственной фермой. Т.к. жесткость и масса конструкции величины не зависимые от внешней нагрузки, то при определении собственных форм и частот колебаний для разных пульсационных загружений имеет место случай кратных форм колебаний, т.е. форм с одинаковой частотой.Если частотное уравнение имеет кратные формы, условие ортогональности форм (вдоль граней башни, в данном случае вдоль глобальных осей Х и У) не справедливо. В этом случае существует целое семейство векторов, любая пара из которых может служить собственными векторами для кратных частот. Эта пара будет ортогональна друг другу, но произвольно повернута вокруг вертикально оси башни:

Т.к. ординаты форм колебаний учитываются при определении величины пульсационной составляющей ветровой нагрузки, то в случае кратных форм последняя будет зависеть от угла поворота перемещения по кратным формам относительно главных осей сооружения. Если учесть, что угол поворота кратных форм величина случайная, то прогнозировать правильность результатов сложно. В данном случае возможно как уменьшение, так и увеличения вклада ветровой пульсации в усилия в элементах схемы.Правильный результат будет получен в случае совпадения направления перемещений по одной из кратных форм с направлением ветровой нагрузки.Для борьбы с кратными формами колебаний применяют разные подходы. Наиболее распространенные из них – изменение геометрии (жесткости) или масс. К примеру, в справке к ПК Abaqus написано:

«In cases with repeated eigenvalues and eigenvectors, the modal summation results must be interpreted with care. You should add insignificant mass to the structure or perturb the symmetric geometry such that the eigenvalues become unique»

«В случаях с повторяющимися собственными значениями и собственными векторами результаты модального суммирования должны интерпретироваться с осторожностью. Вы должны добавить несущественную массу к конструкции или нарушить симметричную геометрию, чтобы собственные значения стали уникальными»

При изменении геометрии башня создается прямоугольного сечения с размерами а и k*a (k принимается 1.01-1.05). При изменении масс по одному из направлений прикладываются дополнительные массы (0.01-0.05 от общей массы сооружения по данному направлению).В ЛИРА-САПР версии 2018 появился новый инструмент Суммирование кратных форм. В случае ветровой пульсации направление итоговой формы колебаний принимается по направлению статической составляющей ветровой нагрузки. Так при ветре, заданном на грань, суммарная форма перемещений также будет на грань. При направлении ветра на диагональ, заданном через 2 составляющие вдоль осей X и Y, итоговое направление формы перемещений будет по направлению равнодействующей, т.е. тоже на диагональ.

Ниже будут показаны варианты расчета башни на действие пульсационной составляющей ветровой нагрузки с учетом суммирования по формам колебаний и без него. Сравниваться будет НДС схемы при определении величины ветровой пульсации «ручным» способом (см. выше) и программно.

Суммирование кратных форм

К башне, описанной выше, прикладывается статическая составляющая ветровой нагрузки. Пульсационная составляющая определяется программно.

Величина узловой нагрузки Wm/4 (Wm см. таблицу 2).Пульсационная составляющая по результатам расчета:

Пульсационная составляющая в уровне отм. +30.000 Wp=0.165*4=0.66тс, что близко к величине нагрузки в таблице 1 (Wp=0.6575тс). Т.е. результаты «ручного» и программного расчета совпадают.Усилия в элементах башни от полной ветровой нагрузки на грань (получено через РСН):

Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на грань, определенная «вручную» и приложенная единой нагрузкой.Ветер на диагональ.

Пульсационная составляющая в уровне отм. +30.000 Wp=Wpx/cos45⁰=(0.14*4)/0.7071=0.792тс, что близко к величине нагрузки в таблице 2 (Wp=0.789тс). Т.е. результаты «ручного» и программного расчета совпадают.Усилия в элементах башни от полной ветровой нагрузки на диагональ:

Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на диагональ.

«Управление» кратными формами

При расчете башни без использования функции «Суммировать формы перемещений» кратными формами колебаний следует управлять, чтобы получить ожидаемый результат. Так при ветре на грань следует задать дополнительные веса масс по направлению воздействия ветровой нагрузки:

Величина дополнительных весов масс принимается 0.01-0.05 от общего веса массы сооружения по данному направлению.В примере выше для каждого уровня принята величина дополнительной массы, пропорциональная массе сооружения на данном уровне.

Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия. Максимальное продольное усилие увеличилось на 100%*(7.15-7.13)/7.13=0.28%.При действии ветра на диагональ следует ввести локальную систему координат узлов по направлению ветра. Для этого нужно отметить узлы, к которым прикладывается нагрузка, вызвать диалог «Локальные оси узлов» и указать в качестве координат точки, из которой будет смотреть ось X2, достаточно большие величины:

В итоге для узлов местные оси Х2 будут параллельны и сонаправлены с ветровым воздействием. Итоговая форма колебаний при определении величины ветровой пульсации также будет совпадать с направлением ветра на диагональ.

Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия.